Poziţia vehiculului reprezintă condiţia geometrică a tuturor componentelor ce contribuie la determinarea poziţiei roţilor în timpul deplasării, fie aceasta în linie dreaptă sau în curbă. Poziţia geometrică poate fi verificată numai în timpul staţionării.
Atunci când autovehiculul se afla în mişcare, datorită stărilor de încărcare variabile, multiple forţe îşi fac apariţia, forţe creată de rezistenţă la înaintare, greutate, accelerare au decelerare create de cuplul motor, forţa centrifugă, frâne, etc. ce tind să modifice poziţia geometrică.
Atunci când se ajustează poziţia geometrică, în concordanţă cu datele furnizate de producător, factorii enumeraţi ai sus sunt luaţi în considerare, dar şi balanţa corectă a forţelor precum şi punctul de aplicare al acestora în timpul mişcării.
Toate acestea înseamnă că adevărata “balanţă a forţelor” poate fi efectuată, exact ca şi cum autovehiculul ar fi în mişcare.
1.1 Condiții de bază ale geometriei vehiculului
Ca și unghiul caracteristic al roților, ce îl vom trata în capitolele următoare, vehiculul trebuie să satisfacă anumite condiții de simetrie și perpendicularitate pe axe, așa cum este arătată în fig. 1

PD si PS = Ampatamentul pe dreapta si stanga, Ca si Cp = Urmele fata si spate
Apatamentul si urmele nu trebuie intotdeauna sa fie egale. De fapt, exista un numat mare de cazuri in care urmele sunt diferite, si, mai putin comun, in care ampatamentele nu sunt egale. Cazuri tipice de amppatamente diferite pot fi gasite pe unele vehicule cu tractiune fata si

Conditia de simetrie a sasiului poate fi verificata in mai multe feluri: o metoda simpla de verificare este proiectarea punctelor de masurare la nivelul solului cu un fir de plumb.
Aceasta trebuie facuta la nivelul solului iar conditia esentiala este ca presiunea in roti sa fie cea indicata de producator.
O alta conditie foarte importanta ce trebuie luata in seama este distribuirea greutatii ce actioneaza asupra vehiculului si efectele nivelului longitudinal si transversala fata de sol, precum si ce arata figurile 3 si 4.


Vehiculul poate fi folosit gol (numai cu şoferul înăuntru) sau cu pasageri, şi cu sau fără combustibil sau bagaje; influenţa acestor condiţii variabile de încărcare asupra compresiei părţilor elastice ale suspensiei, plus efectul anumitor forţe în timpul deplasării autovehiculului, conduc la poziţie variabila a geometriei roţilor.
Tragem concluzia că o cunoaştere aprofundată a geometriei roţilor şi a afectelor generate de contidiile de folosire ale vehiculului este necesară pentru a se face o interpretare inteligentă a datelor furnizate de producător şi a tolerantelor aplicate.
Practica curenta de a masura pozitia geometrica a vehiculului in stare neincarcata, in cazul in care nu se specifica alta metoda de catre producator: acesta este folosita pentru ca masuratorile se pot face rapid si pentru ca aceasta stare, neincarcata, reprezinta cea mai apropiata varianta de conditiile de folosire zilnice ale vehiculului, vehicul ce functioneaza in majoritatea timpului doar cu soferul la bord; o exceptie se iveste atunci cand se verifica daca variatiile produse in timpul incarcarii la maxim a vehiculului ce au ca efect compresia elementelor elastice ale suspensiei altereaza sau nu caracteristicile de elasticitate si pozitionare geometrica.
Înainte de a verifica poziţia geometrică a vehiculului, este esenţial să se observe următoarele condiţii de bază:
1.Localizaţi şi eliminaţi orice joc al suspensiei sau al direcţiei;
2.Poziţionaţi vehiculul pe o suprafaţă plană;
3.Verificaţi presiunea roţilor;
4.Respectaţi şi luaţi în considerare condiţiile specificate de încărcare;
5.Respectaţi şi luaţi în considerare distribuţia sarcinii;
6.Verificaţi dacă exista vreo neregulă asupra părţilor elastice ale suspensiei şi ale rigidităţii articulaţiilor.
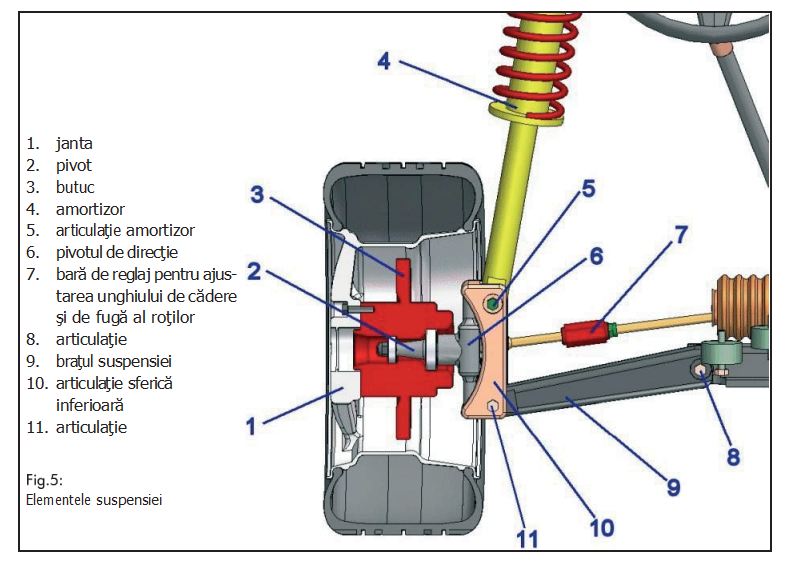
2.1 Suspensiile
Termenul „suspensie” este utilizat pentru a descrie totalitatea pieselor elastice care conectează roţile la şasiu sau la caroseria autoportantă.
Sistemele de suspensie au următoarele funcţii:
Pentru a îndeplini diversele cerinţe de fabricare ale vehiculelor, există mai multe tipuri de sisteme de suspensie: Mac Pherson, mecanism cu articulaţie cu patru bare transversal deformabil, mecanism cu articulaţie cu patru bare longitudinal, tip traversă, etc. Dat fiind că nu este posibil să oferim o descriere detaliată a fiecărui tip în acest document, in fig. 5 puteti gasi o reprezentare schematica a suspensiei, pentru a clarifica denumirile tehnice ale pieselor care alcătuiesc sistemul.
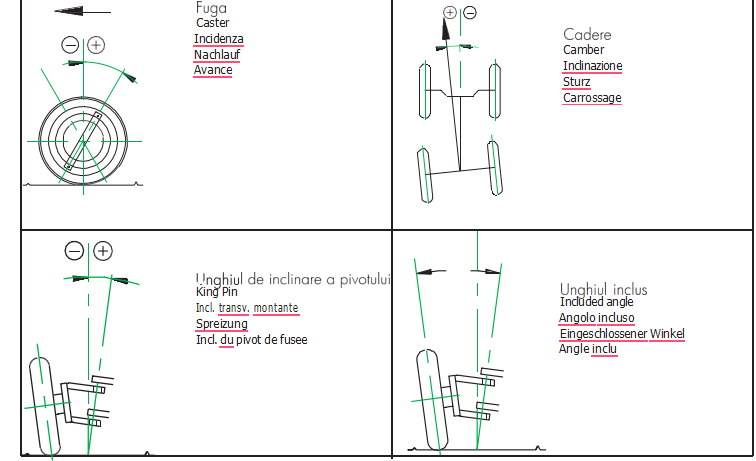
2.2 Unghiuri caracteristice
Unghiurile față de axa frontală sau axa direcţională a vehiculului sunt după cum urmează:
Unghiurile roților:
a)Unghiul de cădere a roţilor;
b)Convergenţa roţilor;
c)Convergenţa negativă a roţilor la viraje.
Unghiuri ale pivotului de direcție:
d)Înclinaţie transversală a pivotului de direcţie, sau pe scurt „înclinaţia pivotului de direcţie”;
e)Unghi longitudinal de fugă a roţilor, sau pe scurt „Unghi de fugă a roţilor”.
Unghiurile roților:
f)Unghi de cădere a roţilor;
g)Convergenţa sau convergenţa negativă a roţilor.
Dat fiind că aceste unghiuri sunt setate de producător, este util să se cunoască terminologia
în diferite limbi.
3.1 Definiții
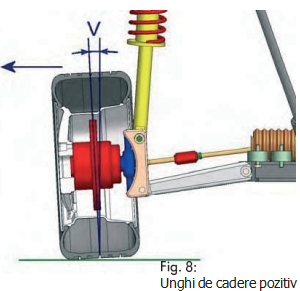
Unghiul de cădere al roţilor este unghiul, măsurat în grade, dintre linia mediană a rotii şi perpendiculară pe sol, atunci când se priveşte vehiculul din fata (fig. 7).
Dacă partea superioară a rotii este aplecata către exterirorul vehicului, unghiul de cădere este POZITIV (fig. 8).
Dacă partea superioară a rotii este aplecata către interiorul vehiculului, unghiul de cădere este NEGATIV (fig. 9).


3.2 Condiții
Să aruncăm o privire asupra motivelor pentru care roata are un unghi de cădere. Dacă pneul ar fi poziţionat perfect pe sol, şi uzura pe suprafaţa de rulare a acestuia ar fi simetrică, atunci roata ar trebui să aibă unghiul de cădere zero (adică perpendiculară pe sol) pentru orice situaţie apărută în timpul rulării. Din moment ce aceste situaţii sunt extrem de variabile existenţa unui unghi de cădere pozitiv sau negativ ajustat corect trebuie conştientizata.
Unghiul de cădere a fost creat pentru a îndeplini cerinţe ce apărute cu mult înaintea automobilului; chiar de pe vreamea căruţelor trase de cai. În acea vreme, roţile erau de diametru mare pentru a face mai uşoară trecerea peste denivelările suprafeţei de rulare, şi în acelaşi timp, din motive de greutate, prezentau spiţe, ataşate butucului (fig. 10).





Pentru a compensa fragilitatea spiţelor, ce se puteau rupe destul de uşor atunci când se trecea peste un obstacol/denivelare, acestea erau înclinate către interiorul vehiculului, dându-le o formă concava. Însă, efectul greutarii putea cauza ruperea acestora fie la îmbinarea cu butucul fie la îmbinare cu cercul de rulare (punctele „A” şi „B” în fig. 11).
Pentru a remedia această problemă, butucul a fost orientat în jos, astfel încât greutatea vehicului este distribuita pe spiţe în positia verticală (fig. 12); în acelaşi timp, forma concava a roţii, foarte rezistentă la impactul lateral cauzat de lovire cu obsacole, a fost menţinută, şi datorită reacţiei (R3) generată de greutate vehiculului, era imposibil că roata să se desprindă de pe butuc, deci putem spune să printr-o modificare s-au rezolvat două probleme.
Autovehiculele au urmat de îndată acest model (fig. 13). Aceasta metodă a folosit în avantajul său faptul că reacţia R3 generată de greutatea vehiculului avea ca efect împingerea rotii către vehicul, deci cum am spus mai sus, desprinderea acesteie era practic imposibilă; dar în acelaşi timp, alte necesităţi au fost create.
3.3 Cauze
În primul rând, datorită vitezei autovehiculelor, s-a ivit nevoia ca rotile să aibă o masă cât mai mică pentru a elimina efectul giroscopic (fig. 14); acest efect, conform legilor fizicii, crează o rezistenţă puternică atunci când se doreşte schimbarea direcţiei corpului supus acestei forţe, şi cu cât mai mare masă şi viteză, cu atât efectul se face simţit mai puternic.
În al doilea rând, s-a ivit nevoia ca numai rotile să se întoarcă, nu toată puntea faţă ca în cazul căruţelor; acest lucru este necesar pentru stabilitatea vehiculului, diferenţa de ampatament dintre punţi fiind mai mică (se evita răsturnarea vehiculului la viteze mari, ca rezultat al forţei greutăţii şi al forţei centrifuge) sau, în acelaşi timp, reducerea dimesiunilor punţii fata, ce a devenit fix (fig. 15).



Aceste probleme sunt depăşite prin montarea roţilor viratoare pe două pivoturi ce facilitează schimbarea direcţiei (fig. 15).
Pivotul este folosit pentru a vira, dar rezistenţa întâlnită în timpul virării creşte o dată cu distanţa dintre punctul de contact al rotii şi proiecţia pivotului pe sol, distanta cunoscută ca “deviaţia pivotului” (distanta “B” în fig. 16); de fapt, un efect de rezistenţă este creat, proporţional cu deviaţia pivotului
“B”, atunci când rezistenta datorită frecării dintre roata şi suprafaţa de rulare acţionează asupra roţii, sau o forţă perturbatoare este generată de impactul cu un obstacol (fig. 16).
Rezultatul „Fp x B” este momentul rezistenţei Mp ce trebuie depăşit pentru a face posibilă virarea rotii; evident, cu cât valoarea “B” este mai mare, cu atât efortul depus în întoarcerea sau menţinerea direcţiei rotii o dată virata este mai mare.
În acelaşi timp, o dată cu creşterea valorii “B”, creşte şi raza de întoarcere şi în consecinţă şi riscul de rupere al butucului, în zona indicată în fig. 16.
În trecut, butucul a fost înclinat în jos pentru a reduce deviaţia pivotului; acestu lucru însă nu este suficient pentru a reduce efectul forţelor perturbatoare, ce afectează direcţia. În acelaşi timp, unghiul de cădere nu a putut fi mărit în aşa măsură încât să se anuleze deviaţia pivotului (fig. 17).
Pentru a reduce interferentele perturbatoare asupra diectiei, presiunea pneurilor a fost scăzută, moficandu-se astfel şi structura acestora. Astfel, contactul dintre suprafaţa de rulare şi roata este mai maleabil.


Însă, efectul unui unghi de cădere mare combinat cu cel al pneului mai moale este unul negativ, din moment ce suprafaţa exterioară a pneului se deformează şi parcurge o distanţă mai mare în curbă decât cea interioară. Rezultatul este uzura neuniforma pe suprafaţa de rulare a pneului (partea exterioară se uzează mai tare, fig. 18). În ilustatie, se poate vedea că suprafaţa de contact a pneului cu solul este una conica, lucru ce face că tendinţa rotii să fie una viratoare către exterior, generând uzura neregulată şi instabilitate în cazul în care unghiurile de cădere ale celor două roţi ale aceleiaşi punţi nu sunt identice.
Aşadar, unghiul de cădere trebuie redus; dar acest lucru ar ducă la mărirea deviaţiei pivotului “B”, şi efectele s-ar simţi şi mai tare atunci când se vor monta şi frâne; de fapt, dacă forţa de frânare nu este aceiaşi pe ambele roti, efectele negative asupra virării sunt comparabile cu efectele forţelor perturbatoare asupra direcţiei.
Soluţia acestei probleme poate fi găsită numai dacă înclinarea roţilor se face opus pivotului, astfel încât proiecţia pivotului să cadă pe zona de contact a pneului cu suprafaţa de rulare (fig. 19)
Acest lucru înseamnă că unghiul de cădere al roţilor poate fi redus considerabil, lăsând un mic unghi pentru a compensa deformarea punţii apăruta din cauza încărcării pe vehiculele echipate cu punţi rigide (fig. 20). În acelaşi timp, acest lucru ar duce la reducerea devierii pivotului (“B” în fig. 19) şi efectelor negative ce le are acesta asupra virării.
De fapt, în fig. 20, se poate vedea că rotile tind să aibă un unghi de cădere egal cu zero atunci când vehiculul, mai exact puntea este supusă unei greutăţi ce o deformează.
O dată cu îmbunătăţirea tehnicilor de fabricare, şi cu introducerea suspensiei cu braţe independente, unghiul de cădere s-a micşorat drastic, tinzând spre o valoare foarte apropiată de zero în conditiie cele mai uzuale de folosire şi încărcare ale vehiculului; trebuie să luăm în seamă că unghiul de cădere tinde să varieze în timpul rulării.
De fapt, în timpul rulării, braţele suspensiei urmează anumite traiectorii, ce au razele r şi R (fig. 21).
Atunci când suspensia este comprimată, poziţia rotii va fi mai ridicată faţă de caroserie; că este destinsa, poziţia rotii va fi mai lăsată faţă de caroseire. În timpul acestor mişcări ale roţii, unghiul de cădere se va schimba de la negativ în timpul compresiei la pozitiv în timpul destinderii; acest lucru este creat de combinaţia factorilor legaţi de deformarea paralelogramului format de braţele superioare şi inferioare ale suspensiei şi de pivotul rotii.
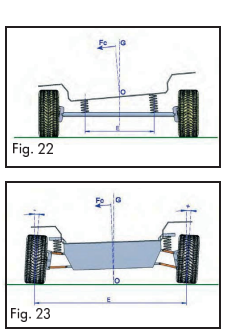
Acesta a fost unul din factorii ce au condus la favorizarea suspensiei independente în defavoarea celei cu ax ridig. Beneficiile acestui efect sunt cel mai bine vizibile în curbe, unde compresia suspensiei roţilor exterioare curbei, cauzată de forţa centrifugă, produce un unghi de cădere negativ asupra rotii şi acţionează contrar forţei de răsturnare a vehiculului; acest lucru nu se întâmplă în cazul vehiculelor echipate cu suspensii cu ax rigid.
Un alt aspect pozitiv al suspensiei independente, ilustrat în fig. 22, este: referitor la distanţa “E”, dintre reacţiile elastice ale celor două sisteme; în cazul suspensiei independente, această distanţă are aceiaşi valoare deci stabilitatea fiind mai bună, comparativ cu sistemul de suspensii cu ax rigid (fig. 23).
Deformabilitatea paralelogramului format de braţul superios şi cel inferior al suspensiei şi pivotul rotii este legată de o serie de raporturi prestabilite.
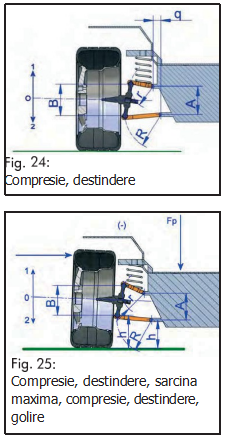
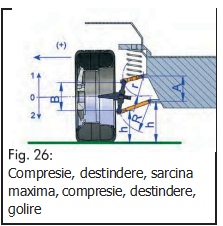
De fapt, în fig. 24, se poate vedea că: Raportul dintre lungimile “r” şi “R” determina gradul de variaţie al unghiului de cădere, fie pozitiv ori negativ, în concordanţă cu deplasarea pe verticală; cu cât este mai mare raportul r/R, cu atât este mai mare variaţia unghiului de cădere la o deplasare minoră pe verticală.
Distanţa “q” este reglată în funcţie de lungimea braţelor “r” şi “R”, pentru a da înclinaţia corectă a pivotului. Unghiul de cădere pozitiv sau negativ este determinat de distanţele “A” şi “B”, adică, dacă acestea sunt sau nu la fel (braţe paralele); şi de poziţia braţelor faţă de sol în condiţii normale de folosire ale vehiculului. Dacă, de exemplu, se decide că roata să aibă unghiul de cădere zero în condiţii normale de încărcare şi folosire, acest lucru, evident acest lucru înseamnă că roata se afla în punctul de mijloc dintre compresia totală şi destinderea totală, cu alte cuvine, la aceiaşi distanţă atât faţă de comprimarea totală cât şi de destindetea totală. În acest caz, unghiul de cădere va tinde către
o valoare pozitivă când vehiculul este gol, şi către o valoare negativă când vehiculul este încărcat.
Când braţele suspensiei sunt în poziţia clasică, aşa cum este arătat de poziţiile 1 şi 2 ale fig. 25, condiţia descrisă mai sus va fi satisfăcută.
De fapt, cu braţele suspensiei astfel reglate, ceea ce înseamnă că distanţa “A” va fi diferită de distanta “B”, pentru un minim de deplasată în sus sau în jos al roţii, unghiul de cădere inevitabil va varia.
Din mai multe motive, nu este întotdeauna posibil ca producătorul să respecte regulile aranjamentului clasic; de aici, modurile de aranjare ale braţelor sunt foarte multe, şi pentru a se evita calcule complexe cu privire la aranjarea geometrică, se recomandă să se respecte următoarele proceduri atunci când se stabileşte unghiul de cădere:
3.5 Exemple
Unghiuri de cădere specificat de producător: +0°20′ şi +1°, cu autovehiculul gol.
Primul caz
Şoferul călătoreşte predominant singur (greutatea pe stânga) şi roţile tind să reducă unghiul (spre negativ) sub compresie. Atunci când se ajustează unghiul de cădere, se recomanda: unghiul rotii din stânga (deci cel de pe partea şoferului) se ajustează la
+1°, iar cel de pe partea drepta, unde vehiculul este mai uşor, se ajustează la 0°20′.
Al doilea caz
Şoferul călătoreşte predominant singur (greutatea pe stânga) şi roţile tind să crească unghiul (spre pozitiv) sub compresie. Atunci când se ajustează unghiul de cădere, se recomanda: unghiul rotii din stânga (deci cel de pe partea şoferului) se ajustează la 0°20′, iar cel de pe partea drepta, unde vehiculul este mai uşor, se ajustează la +1°.
4.1 Definiții
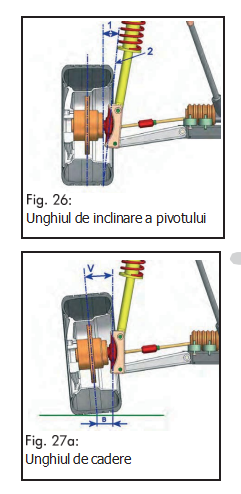
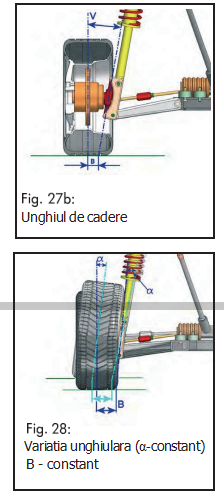
Înclinaţia pivotului este unghiul, măsurat în grade, format intre linia mediană a pivotului şi perpendiculară pe sol, privind vehiculul din fata (fig. 26).
Unghiul de cădere a fost inventat pentru a reduce deviaţia pivotului, resprezentata de distanta “B” dintre proiecţia axei pivotului pe sol şi punctul de contact al rotii (cap. 3 pag XX), dar s-a observat că o mărire a acestui unghi crează efecte negativă, în special când se folosesc rotile cu cauciucuri fără camera/tubeless.
Astfel, s-a simţit nevoia reducerii unghiului de cădere foarte mult, aproape de valoarea zero; lucru necesar şi pentru a obţine o uzură uniformă a cauciucurilor. Problema a fost rezolvată prin inclinarea pivotului către partea de jos a rotii (fig. 27).
În cazul suspensiilor cu punte rigidă, înclinaţia pivotului nu variază sub efectul greutăţii şi deplasării pe verticală a roţii, cu condiţia ca axul să nu se deformeze; în cazul suspensiei independente, greutatea şi mişcarea pe verticală a vehiculului face că atât unghiul de cădere cât şi înclinarea pivotului să varieze în aceiaşi măsură, din moment ce pivotul se mişcă o dată cu butucul rotii (fig. 28).
Inclinarea pivotului este considerată pozitivă atunci când proiecia axului pivotului ajunge aproape de punctul de contact al rotii cu suprafaţa de rulare (înclinată în partea opusă unghiului de cădere); este dificil, dacă nu imposibil să avem o înclinaţie negativă a pivotului.
4.2 Unghiul inclus
Unghiul dintre axa pivotului şi axa rotii este egal cu suma algebrica a unghiului înclinaţiei pivotului şi a unghiului de căderea şi este definit că unghiul inclus (fig. 29).
EXEMPLU
Primul caz
Unghiul de cădere +2°, Unghiul înclinaţiei
pivotului +6°, deci unghiul inclus +8°
Al doilea caz
Unghiul de cădere -1°, Unghiul înclinaţiei
pivotului +8°, deci unghiul inclus +7°
Unghiul inculs poate varia numai dacă există o deformare intre axa pivotului şi butucul rotii (“F” şi “G” în fig. 29). Dacă, în timpul operaţiilor de verificare, se observa că unghiul înclinaţiei pivotului şi unghiul de cădere diferă considerabil de valorile specificate, atunci, înainte de a decide ce acţiune trebuie efectuată sfătuim să verificaţi dacă unghiul inclus a rămas neschimbat.
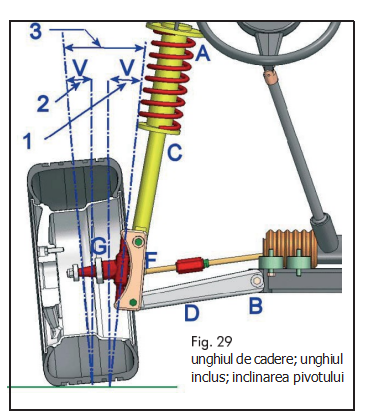
Exemplu Valori specificate Valori asociate
| Unghiul de cădere | +2° | +1° (mai mic decât spec.) |
| Inclinatia pivotului | +6° | +7° (mai mare decât spec.) |
| Unghiul inclus (+2°+6°) = | +8° | +8° constant |
În acest caz, deformarea uşoară, sau poziţionarea anormală a părţilor va fi legată fie de braţele suspensiei fie de suportul braţelor (detalii „A”, „B”, „C” şi „D: în fig. 29). În acest caz poziţionarea pivotului şi bucutului nu s-au schimbat.
Dacă, pe de altă parte, sunt observate următoarele unghiuri:

Exista o defromare în ansamblul pivot-butuc (detalii “F” şi “G” în fig. 29).

Unghiul de înclinare al pivotului, printre altele, crează fenomenul de întoarcere al roţii în poziţia de mers înainte; de asemenea, tinde să menţină această poziţie după un impact cu un obstacol.
Acest efect natural, care este de o importanţă vitală, datorită înclinaţiei pivotului, derivă din faptul că roata, atunci când se învârte în jurul acestei axe oblice, formează un con cu vârful în jos, aşa cum este arătat în fig. 30.
Se poate vedea din fig. 30 ca, atunci când butucul este în poziţia 1, se afla în cel mai înalt punct în raport cu solul şi roata este în poziţia de mers înainte.
Atunci când virăm câte dreapta sau stânga, poziţiile 2 şi 3, bucutul coboară, şi în consecinţă roata tinde să se ducă sub nivelul solului; din moment ce aşa ceva
este imposibil, tendinţa este de a ridica caroseria într-o poziţie instabilă. Astfel, atunci când întoarce volanul, şoferul nu numai că întoarce rotile dar, de asemenea, datorită efectului creat de greutate, ridică şi caroseria vehiculului; imediat cum şoferul încetează să mai ţină volanul, caroseria, datorită tendinţei naturale create de propria greutate, revine în punctul cel mai jos, şi, împreună cu această mişcare, face că rotile să revină în poziţia de mers înainte. Evident, cu cât vehiculul este mai greu sau mai mare înclinaţia pivotului, cu atât forţă necesară virării şi viteaza de revenire sunt mai mari.
Astfel, fiecare forţa perturbatoare (Fp) asupra direcţiei de mers înainte a roţilor va întâlni o forţă egală de sens contrar, datorită greutăţii vehiculului, acţionând în direcţie transversală de-a lungul axei pivotului oblic, şi astfel, contribuind enorm la conservarea stabilităţii vehiculului (Fig. 31).
5.1 Definiții
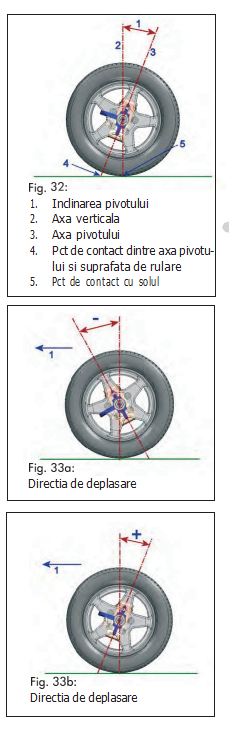
Unghiul de fuga este unghiul, măsurat în grade, format între axa pivotului şi perpendiculară pe sol, privind vehiculul din lateral (fig. 32).
Din moment ce acest unghi este format longitudinal în raport cu vehiculul, cea mai exactă definite este: unghiul longitudinal de fugă. În utilizarea practică este cunoscut pur şi simplu că “unghi de fugă”.
Prin convenţie s-a stabilit că, dacă extensia axei pivotului cade în fata punctului de contact al roţii cu suprafaţa de rulare, unghiul de fuga este definit ca POZITIV, şi dacă aceasta cade în spatele punctului de contact al roţii cu suprafaţa de rulare unghiul de fuga este definit ca fiind NEGATIV. Unghiul de cădere este zero dacă pivotul este perfect vertical (fig. 33).
Unghiul de fugă dat de pivot crează două tendinţe/fenomene foarte importante ale rulării vehiculului: prima tendinţa este legată de stabilitate, menţinând linia dreaptă de rulare a vehiculului, cu revenirea relativă a roţilor după o curbă, şi al doilea este înclinarea roţii în timpul virării.
5.2 Stabilitatea
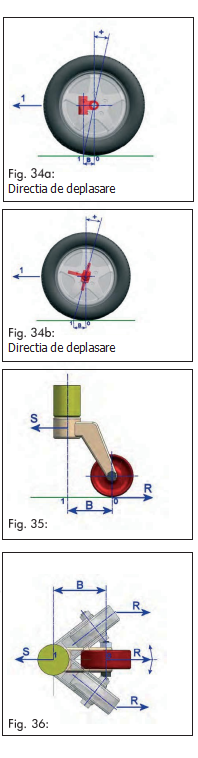
Acest fenomen este creat datorită distanţei “B”, distanţa dintre punctul de proiecţie al axei pivotului, punctul “1” (în raport cu direcţia de mers) şi punctul de contact al pneului cu suprafaţa de rulare (fig. 34).
Fig. 34 arată două roţi cu unghi de fugă pozitiv (extensia pivotului cade înaintarea punctului de contact al pneului cu suprafaţa de rulare) folosind două sisteme: unul este de a înclina pivotul şi celălalt este de a muta poziţia pivotului în raport cu axa roţii. Stabilitatea la mersul în linie dreaptă este prezentă în ambele cazuri.
De fapt, în cazul unghiului de fugă pozitiv, roata este trasă, din moment ce este în linia de acţiune a forţei aplicate asupra axului, forţa ce trece prin punctul 1 aflat în fata roţii (fără a lua în considerare direcţia de mers fig. 35).
Orice încercare a roţii de a devia de la direcţia de mers (în linie dreaptă) va fi contracarată de cuplul de îndreptare generat de forţă “S” şi de rezistenţă la rulare a roţii “R” (fig. 35).
Însă, în cazul unghiului de fugă negativ, roata este împinsă, din moment ce este pe linia de aplicare a forţei ce acţionează asupra axului, forţa ce trece prin punctul 1, punct aflat în spatele rotii (fără să luăm în considerare direcţia de mers fig. 36)

Orice încercare a rotii de a devia de la direcţia de mers (în linie dreaptă) va fi ajutata şi amplificată de cuplul generat de forţa “S” şi de rezistenţă la rulare a rotii “R” (fig. 36).
În consecinţă, cea mai bună condiţie de stabilitate pentru mersul în linie dreaptă a rotii este obţinută cu un unghi de fugă pozitiv şi deci, tragerea rotii; de fapt, în acest caz, fenomenul de oscilare al rotii şi efectele negative ale acestuia sunt înlăturate.
Să examinăm acum ce se întâmplă cu roata în timpul virării. În cazul unghiului de fugă cu valoare zero, axa de întoarcere va coincide cu punctul de contact al pneului cu suprafaţa de rulare (fig. 37). În acest caz comportamentul rotii este unul neutru, şi este sensibil la toate forţele perturbatoare ce încearcă să modifice traiectoria dreaptă a acestora (şi deci instabilă), şi în consecinţă nu prezintă tendinţa de revenire la direcţia de mers înainte după efectuarea unei curbe.
Dacă roata are un unghi de fugă pozitiv, atunci când este întoarsă în jurul axei pivotului îşi schimba punctul de contact cu suprafaţa de rulare şi, în consecinţă, punctul în care rezistenta la înaintare “R” este aplicată, precum este arătat în fig. 38; forţa “S”, însă, întotdeauna acţionează în aceiaşi direcţie.
Acest lucru conduce la crearea cuplului de întoarcere “Mr” de către forţele “R” şi “S” ce tind să readucă roata în poziţia de mers înainte (fig. 38).
Dacă unghiul de fuga este negativ, atunci când roata este întoarsă în jurul axei pivotului îşi schimbă punctul de contact cu suprafaţa de rulare şi, în consecinţă, punctul în care rezistenta la înaintare “R” este aplicată, precum este arătat în fig. 39; forţa “S”, însă, întotdeauna acţionează în aceiaşi direcţie.
Acest lucru conduce la crearea cuplului de către forţele “R” şi “S” care, în contrast cu cazul anterior, tind să amplifice efectul virării roţilor şi împiedica revenirea acestora în poziţia de mers înainte.
Comportamentul diferit al roţilor cu unghi de fugă pozitiv şi negativ poate fi verificat practic prin conducerea aceluiaşi vehicul înainte şi înapoi; mai exact, atunci când vehiculul merge înainte şi are un unghi de fugă pozitiv, rotile vor reveni în poziţia neutră după efectuarea unui viraj, lucru care nu se va întâmpla după efectuarea unui viraj în marşarier; în cazul unghiului de fugă negativ, lucrurile vor fi exact invers, şi anume rotile vor reveni numai după efectuarea unui viraj în marşarier.
În cele două cazuri ilustrate în fig. 38 şi 39, se poate vedea că, cu cât mai mare unghiul de fugă (fie el pozitiv sau negativ) cu atât mai mare va fi deplasamentul longitudinal “B” şi translaţia punctului de aplicare al forţei rezistente în timpul virării “R”. De aceea, se poate trage concluzia că, cuplul Mr este atât cel care ajută la îndreptarea roţilor (fig. 38) cât şi la auto-virare (fig. 39), şi este direct proporţional cu deplasamentul longitudinal “B”.

În cel mai comun caz, cel cu unghi de fugă pozitiv, cuplul Mr, ce crează efectul de revenire al roţilor, va acţiona contrat forţei impuse de şofer de a vira; astfel, se poate spune că: cu cât mai mare valoare unghiului de fugă pozitiv, cu atât mai mare forţă necesară a fi aplicată pentru a vira, însă, în acelaşi timp, stabilitatea în cazul direcţie de mers înainte, atunci când vor interveni forţe perturbatoare, va fi mai mare.
Dacă unghiul de fuga este diferit pe cele două roţi ale aceluiaşi ax (cauzând reacţii diferite în cazul varierii traiectoriei), vehiculul va tinde să devieze singur de la traiectorie, către partea unde unghiul este mai mic, în valoare absolută; acest efect este simţit mai puternic în timpul accelerării şi frânării.Acest lucru este ilustrat clar în fig. 40.
Fenomenul de revenire în poziţia de mers înainte este garantat de înclinaţia transversală a pivotului; faptul că unghiul de fugă contribuie şi el la acelaşi efect ajuta. În cazul autovehiculele tradiţionale, unghiul de fugă tinde către zero, şi este mai mare numai pe vehiculele care prezintă o sarcină mică pe rotile viratoare.
5.3 Fenomenul incalinării cu rotile in pozitia de virare

În capitolul în care am vorbit despre unghiul de cădere al roţilor, se poate vedea că acest unghi variază în concordanţă cu poziţia sau lungimea braţelor suspensiei sub efectul compresiei şi destinderii (fig. 21).
Acest efect este foarte folositor atunci când virăm, atunci când forţa centrifugă ce deformează paralelogramele (formate de braţele suspensiei) modifica unghiul de cădere, negativ pentru roata exterioară virajului şi pozitiv pentru cea interioară (fig. 22).
Acelaşi rezultat este obţinut pentru rotile ce prezintă unghi de fugă. În fig. 41 se poate vedea că roata, care se presupune a fi în poziţia OA cu unghi de cădere 0°, atunci când este rotită în jurul axei pivotului, ce are un unghi de fugă reprezentativ “i”, după o întoarcere cu 90°, va fi poziţionată în punctul OB cu unghiul de cădere egal cu cel de fugă, ambele negativ. Atunci când virează cu 90°, dar de la poziţia OA la poziţia OC, unghiul de cădere va fi tot la fel ca cel de fugă, însă cu valoare pozitivă.
În cadrul mişcării de la OA către OB, roata, în acelaşi timp, tinde să se ridice de la sol; pe de altă parte, atunci când mişcarea are loc de la OA către OC roata va încerca să intre sub nivelul solului. Din moment ce acest lucru nu este posibil, caroseria va fi cea care se va lăsa în raport cu roata, în primul caz, şi se va ridica în al doilea.
Se poate trage următoare concluzie: atunci când roata se întoarce în jurul axei pivotului cu unghi de fugă pozitiv, dacă este în poziţia exterioară curbei, va căpăta unghi de cădere negativ ce creşte o dată cu unghiul de virare, şi astfel va acţiona împotriva răsturnării vehiculului; dacă, pe de altă parte, se afla în interiorul curbei, va căpăta unghi de cădere pozitiv, ce urmează şi asista la virare.
În consecinţă, când vehiculul urmează o curbă largă la o viteză foarte mare, forţa centrifugă, prin deformarea paralelogramelor va fi cea care ajută la poziţionarea pe şosea; când curba este foarte strânsă şi viteză moderată, unghiul de fugă va fi cel ce va determina modificarea unghiului de cădere pentru a ajuta în urmărea traiectoriei.
5.4 Alti factori care influenteaza unghiul de fuga
Pneurile de joasă presiune (tubeless), de pe vehiculele moderne, contribuie la reducerea unghiului de fugă datorită unghiului dat pivotului în timpul construcţiei; de fapt, atunci când se afla sub influenţa accelerări sau frânarii, pneul se deformează şi tinde să mărească deplasarea longitudinala prin modificarea punctului de contact cu suprafaţa de rulare (fig. 43).
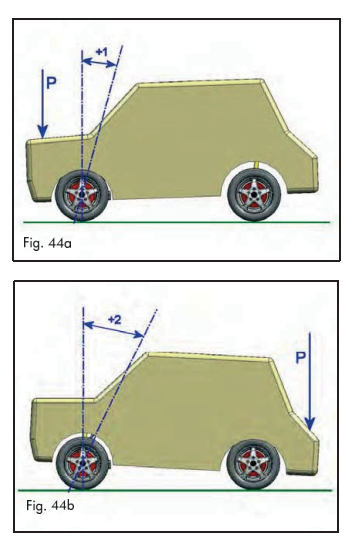
Unghiul de fugă variază de asemenea o dată cu varierea distribuţiei greutăţii vehiculului; dacă greutatea este mutată pe puntea spate atunci unghiul de fugă pozitiv va creşte, iar dacă este mutată pe puntea faţă acesta se va micşora (fig. 44).
6.1 Definitii
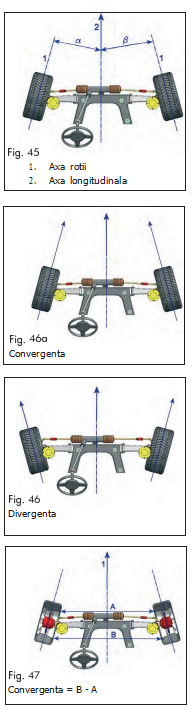
Convergenta roţilor este unghiul format de linia mediană a vehiculului (lina ce trece longitudinal prin centrul acestuia) şi linia mediană a roţilor atunci când privim vehiculul de sus.
Suma valorilor convergentei a fiecărei roti (α+β) da convergenta totală (fig. 45). Atunci când extensia linilor centrale ale roţilor tind să se întâlnească în fata vehiculului, atunci spunem că avem convergenta pozitivă; dacă acestea tind să se unească în spatele vehiculului, atunci spunem că avem convergenta negativă (fig. 46).
Când liniile mediane ale roţilor sunt paralele cu linia mediană a vehiculului spunem că avem convergenta zero.
Convergentă negativă este rareori dată în grade de către producător, este mai comun să se dea valoarea exprimată în mm, valoare măsurată între jantele roţilor; cele două măsurători se fac în faţă şi în spatele butucului, la jumătatea înălţimii jantelor/roţilor.
Dacă B este mai mare că A, rotile se afla în poziţia de convergenţă pozitivă. Dacă A este mai mare că B, rotile se afla în poziţia de convergenţă negativă. Dacă B este egal cu A, rotile se afla în poziţia zero.


6.2 Măsuratori
Când convergenta este măsurată în grade, pentru a se reveni la valori în mm, trebuie luat în considerare diametrul jantei .
Se poate vedea în fig. 48 ca, cu aceeaşi valoare unghiulară (α+β), convergentă, dată de diferenţa (B-A), este evident mai mare în cazul jantelor de 16 inchi faţă de cele de 10 inchi.
Valoarea convergentei stabilită de producător este considerată în aşa fel încât, atunci când se circulă în condiţii normale de sarcină tinde către zero.
De fapt, sub efectul sarcinii, ce deformează paralelogramele suspensiei (vezi cap. 4 fig. 24), sub efectul cuplului motor ce poate fi sau nu aplicat roţilor în cauză şi sub efectul rezistenţei la înaintare, valorile convergentei variază foarte mult.
6.3 Efectele sarcinii asupra convergentei

În cap. 3, în care am tratat unghiul de cădere, este descris comportamentul paralelogramelor suspensiei sub sarcină şi, variaţiile unghiulare produse asupra roţii şi pivotului.
Din moment ce aceste variaţii se bazează pe poziţionarea pivotului, cu înclinarea şi unghiul sau de fugă caracteristic, putem spune că mişcarea suspensiei cauzează variaţii notabile ale valorii convergentei (fig. 49).
Varierea valorii convergentei mai poate fi cauzată de poziţia barei de direcţia în raport cu rotile.
Mişcarea verticală a roţii în raport cu şasiul este urmată de bara de direcţie, care, presupunând că este lăsată de articulaţie, urmează circumferinţa arcului de raza Rt, raza egală cu lungimea barei de direcţie (fig. 50).
Cazurile diferite posibile variază prin faptul că barele de direcţie şi braţele suspensiilor sunt în mod normal de lungimi diferite şi cu puncte de aplicare diferite, ce variază de la vehicul la vehicul.
De fapt, sunt multe tipuri de paralelograme de direcţie, datorită numărului mare de soluţii adoptate de producători; din acest motiv, nu este posibil să avem o regulă exactă despre variaţia convergentei în funcţie de greutate.
Atunci când măsuram convergentă, este indicat să consultam specificaţiile producătorului şi să verificăm dacă tendinţa de modificare a convergentei este pozitivă sau negativă atunci când mişcăm vehiculul în sus şi în jos pe verticală; după aceasta, setaţi tolerantele şi valorile specificate de producător pentru condiţii uzuale de folosite.

6.4 Sistemele Jeantaud & Panhard
În următoarele exemple clasice de paralelograme de direcţie (sistemele JEANTAUD şi PANHARD) se poate vedea că sistemele manifesta comportament diferit al convergentei, datorită faptului că barele de direcţie sunt în poziţii opuse în raport cu puntea faţă (fig. 51 şi 52).
6.5 Efectele dimanice asupra convergentei
Când vehiculul se mişca în linie dreaptă, rotile viratoare, ce nu sunt şi propulsoare şi deci nu sunt influenţate de cuplul motor, tind să adopte o convergenţă negativă sub influenţa rezistenţei la înaintare, Aceasta convergenta negativă este în mod natural premisa de totalitatea jocurilor din sistemul de direcţie şi de suspensie dar şi de flexibilitatea bucşelor.
Se poate vedea în fig. 53 că rezistenţa manifestată de suprafaţa de rulare, care variază în raport cu cuplul motor (acesta acţionează asupra părţii interioare a roţii), se combină cu cuplu pentru a genera o forţă ce tinde să modifice convergenta rotile (spre negativă): în cele mai multe cazuri, pentru a compensa acest efect, este necesară o convergenţă pozitivă în timpul staţionării.
Când, pe de altă parte, rotile viratoare sunt influenţate direct de cuplul motor, deci sunt propulsoare, acestea tind să creeze o convergenţă pozitivă.
În fig. 54 se observă cuplul motor ce trece prin arborele cardanic şi articulaţie direct la butucul roţii; în consecinţă, de data aceasta cuplul acţionează asupra părţii exterioare a pivotului, creând un cuplu de forţă cu rezistenţa Rm, datoria inerţiei vehiculului, ce tinde să tragă spre interior roată. În cele mai multe cazuri, pentru a compensa acest efect, este necesară o convergenţă negativă în timpul staţionării.
General vorbind, următoarele concluzii pot fi trase pentru vehiculele cu suspensie independentă:
Rotile fata sau spate care nu sunt propulsoare au convergenta pozitivă în timpul staţionării;
Rotile fata sau spate care sunt propulsoare au convergenta negativă în timpul staţionării.

6.6 Alunecarea roții
Convergentă mai poate fi exprimată şi în alt fel, dupa
cum se poate observa in fig. 55:
Dacă roţii supuse unghiului de convergenţă i se permite să ruleze liberă, fără vreo formă de impediment, în direcţia generată de convergenţă în raport cu axa longitudinală a vehiculului, după o anumită distanţa aceasta se va afla în altă poziţie faţă de cea în care se afla în realitate, poziţia din realitate fiind forţată de greutatea vehiculului şi rezistenţa creată de cealaltă roata a aceluiaşi ax.
Este evident din fig. 55 ca, după ce a rulat 1km, roata liberă va fi în poziţia B, dar reacţia celeilalte roti o forţează să ajungă în poziţia A; astfel, pentru fiecare întoarcere/rotire, roata efectuează o mişcare laterală care, bazată pe distanţă de un kilometru are o valoare egală cu segmentul A’B, segment ce creşte în concordanţă cu mărimea valorii de convergenţă.
Mişcarea laterală este definită ca ALUNECARE A ROŢII, şi poate fi măsurată în grade, mai exact unghiul format de axă longitudinală a vehiculului cu axa de direcţie a axului roţii; pentru o valoare în metri, segmentul A’B este măsurat la o anumită distanţă Ă’A. S-a stabilit prin convenţie că alunecarea roţii se măsoară în metri pe kilometru, ceea ce înseamnă câţi metri alunecă roată la fiecare kilometru parcurs de vehicul.
Fig. 56 conţine o reprezentare a sistemului, în care:
Se poate stabili următoare relaţie proporţională: φ :km=C:D de unde
Convergentă (m) = [φ (m) x D(m)]/1km(1000m)

Pentru a converti în mm fără a parcurge toţi paşii, sfătuim să folosit formulă:
Convergentă (mm) = Alunecarea în m/km x
Ṣ într-un metru
Exemplu: se dă alunecarea de 6m/km şi diametrul jantei de 12″, convergenţa va fi: 12″=0.3m
Convergenta=6 x 0.30 = 1.8 mm
Pentru a trece de la convergenţă la alunecare, folosiţi aceiaşi formulă:
Alunecarea în m/km = Convergenţa în mm/
Ṣ într-un metru
Exemplu: se dă 12″ diametrul jantei şi convergenţa de 2 mm, alunecarea va fi:
12″=0.3m
Alunecarea=(2:0.3)=6.6m/km
În cazul convergenţei negativă, alunecarea va fi negativ.
6.7 Uzura neuniforma a peurilor
Uzura pricinuită unui pneu cu convergenţă excesivă prezina unele caracteristici tipice: O roată cu convergenţă pozitivă excesivă tinde să se târască din interior către exterior, astfel ca, după o scurtă distanţă de rulare produce un tipar de uzură ce este atât vizibil cât şi palpabil (fig. 57)
Pe de altă parte, o roată cu convergenţă negativă excesivă tinde să se târască de la exterior către interior, astfel că, tiparul produs este de direcţie opusă faţă de cazul anterior (fig. 58).
7.1 Definitii si conditii

Unghiurile caracteristice, tratate anterior, poziţionează roţile precis în timpul rulării în linie dreaptă; pe lângă acest lucru, mai sunt câteva efecte particulare simţite în timpul negocierii unei curbe.
Când roţile sunt bracate, o altă condiţie foarte importantă este creată, condiţie legată direct de raza curbei negociate.
Pentru a înţelege această condiţie, este mai bine să considerăm viteza de rulare a roţii una foarte mică, fără interferenţe; în această situaţie nu există forţe perturbatoare ce acţionează asupa vehiculului, cum ar fi, forţa centrifugă, împingerea laterală datorată vântului, forţe acceleratoare datorate cuplului motor, etc.
O condiţie esenţială, pentru a preveni că roata să fie supusă frânării laterale ce ar fi foarte dăunătoare pneului, este ca, atunci când urmează traiectoria impusă, aceasta trebuie să fie perfect perpendiculară pe raza curbei.


Atunci când toată puntea faţă virează, cu toate că roţile parcurg două cercuri de raze diferite, ele se menţin perpendiculare pe raza arcului de cerc descris de curbă (fig.
60).
Atunci când tot autovehicul este cotit trebuie să se respecte aceleaşi condiţii, ceea ce înseamnă că două axe trebuie să respecte condiţiile simultan, iar puntea spate trebuie să învârtă în jurul aceluiaşi centru de rotaţie (fig. 61).
Această condiţie poate fi respectată cu uşurinţă în cazul în care toată puntea faţă se roteşte, precum este arătat în fig. 61. Însă, din motive evidente de stabilitate şi restricţii de spaţiu sub vehicul, acest lucru nu este posibil în cazul vehiculelor motorizate; vehiculele motorizate sunt virate datorită articulaţiilor pivoţilor; roţile se comportă ca şi cum ar fi pe două punţi separate (fig. 62).
Dar, dacă ambele roţi sunt virate în acelaşi mod, ca în fig. 62, cu un unghi Ṣ, ce urmează două traiectorii diferite dar de aceiaşi rază atunci una din roţi va fi târâtă spre punctul impus de celelalte trei şi astfel uzura cauciucului ce echipează acea roată va fi foarte mare.

7.2 Covergenta in curba
Din fig. 63 se pot vedea următoarele:
DE – traiectorie incorectă a roţii exterioare care, urmând raza Re nu trece prin centrul real al curbei C; acest lucru se întâmplă dacă roata se întoarce cu acelaşi unghi şi Re şi Ri sunt pralalele ca şi DE şi FG.
AB – traiectoria exactă a roţii exterioarea ce urmează raza Ri ce trece prin centrul curbei C; această conditiie poate fi îndeplinită numai atunci când unghiul de întoarcere al roţilor nu este acelaşi, Ṣ şi ß, ceea ce înseamnă că Ri şi Re nu sunt paralele; observaţi de asemenea că roţile trebuie să aibă convergenţă negativă pentru a evita tărârea uneia dintre ele.
Astfel, geometria direcţiei este definită ca poziţia de convergenţă negativă luată în timpul virării; este exprimată în două moduri, primul fiind în grade, garde de întoarcere a roţii (considerând o valoare fixă a întoarcerii de 20°, stabilită prin convenţie).
Exemplu: fig. 64: roata exterioară virajulului se roteşte cu 20° iar cea interioară cu 23°, sau vice-versa, cea interioară se roteşte cu 20° iar cea exterioară cu 17°. În acest exemplu se poate vedea că valoarea convergenţei în cazul unghiului de bază de 20° este de 3°, rezultată din diferenţă (20°-17°) sau (23°-20°).
Astfel, conditiia ideală este: Cele două roţi, ce merg în linie dreaptă, trebuie să aibă o valoare de convergenţă negativă aproape de valoarea 0°, dar, imediat cum încep să negocieze o curbă, valoarea convergenţei trebuie să crească progresiv, devenind mai accentuată o dată cu creşterea unghiului de întoarcere.

7.3 Paralelogramele directiei
Convergentă negativă a roţilor, proporţională cu raza de întoarcere, este generată de cele două bare de direcţie ataşate pivotului, cu lungimi şi poziţii bine definite.
Dacă, însă, cele două bare de direcţie formează un paralelogram articulat simetric pentru ambele roţi ale aceleiaşi punţi, atunci condiţia nu va fi satisfăcută (fig. 65).
ACI MAI INTRI FIG 67 ŞI 68 DE LA
PAGINA 43
De fapt, se poate vedea din fig. 65 că barele de direcţie sunt paralele cu axa longitudinală a vehiculului, şi ele rămân paralele şi în timpul virării; acelaşi lucru se întâmplă şi cu roata, care nu este capabilă să adopte poziţia de convergenţă negativă necesară.
Fig. 66
Convergentă necesară în timpul întoarcerii poate fi obţinută numai dacă cele două bare de direcţie formează un paralelogram asimetric, ceea ce înseamnă că barele de direcţie converg către spatele vehiculului (vezi sistemele Jeantaud şi Panhard).
7.4 Centrul de rotatie instantanee
În cazul paralelogramelor de direcţie asimetrică, atunci când este negociată o curbă, o dată cu mişcarea barelor de direcţie, arcele de cerc descrise de acestea au raze diferite. Acest lucru se întâmplă în fig. 67, unde bara de direcţie de pe partea dreaptă urmează o traiectorie mai idepartata de axa longitudinală XX, şi, în acelaşi timp, bara de direcţie de pe partea stângă se apropie de axa YY; rezultatul se traduce prin faptul că bara de direcţie dreapta urmează arcul AB, creând un unghi Ṣ, iar bara de direcţie stânga urmează arcul A1B1 crand un unghi = 1 mai mică ca Ṣ.
Acelaşi efect este observat, mult mai uşor, dacă arcele BC şi B1C1 au unghiurile ß şi ß1. Se poate trage concluzia că, cu paralelograme de direcţie asimetrice, diferenţa de întoarcere dintre roata interioară şi cea exterioară este dobândită, astfel producând o convergenţă progresivă în raport cu unghiul curbei negociate.
Condiţia teoretică care leagă geometria direcţiei roţilor faţă (viratoare) de poziţia roţilor spate (non viratoare), lucru necesar pentru a evita târârea acestora din urmă, este ca extensia axei barelor de direcţie să se întâlnească exact prin centrul punţii spate (fig. 68).
Unghiul Ṣ adoptat de barele de direcţie devine o funcţie a ampatamentului vehiculului şi în consecinţă a raportului P/C. O dată ce aceste condiţii teoretice au fost îndeplinite, rotiţe, atunci când virează, adoptă o poziţie perpediculara pe raza traiectoriei curbei şi nu sunt supuse nici unei alunecări/târâri laterale ce este atât de dăunătoare pneului (fig. 69).

7.5 Centrarea directiei
Centrarea direcţiei este reprezentată de condiţia de simetrie perfectă a părţilor direcţiei în raport cu axa longitudinală a vehiculului.
Direcţia vehiculului este centrată atunci când barele de direcţie converg către centrul punţii spate(fig. 70):
Axele ce trec prin roţile faţă (indiferent dacă au sau nu convergenţă) sunt simetrice în raport cu roţile spate (distanţă A); Bara de direcţie, pivotul şi direcţia revin în poziţia centrală; Barele de direcţie ajustabile au aceiaşi lungime (distanţa B); Atunci când direcţia este centrată, geometria direcţiei este perfect simetrică, fie că virăm stânga sau dreapta. Acelaşi lucru se aplică în raport cu limita maximă de întoarcere a roţii.


7.6 Devierea axelor
Condiţia teoretică în care proiecţia roţilor faţă pe puntea spate este simetrică A=A’ (fig. 71), roţile viratoare şi sistemul de direcţie sunt în centrul razei de mişcare şi barile de direcţie ajustabile sunt de aceiaşi lungime nu poate fi întotdeauna respectată datorită deformaţiilor sau deviaţiilor ce apar asupra întregului sistem, deformaţii cauzate de neregularităţi ale suprafeţei de rulare.
Aceste deviaţii pot fi grupare în trei categorii, cu toate că sunt unele tipuri de deviaţii care pot fi identificate şi rectificate numai folosind sisteme legate de rectificarea şasiului sau caroseriei.
1)Puntea faţă este oblică în raport cu axa logitudinala a vehiculului şi are o valoare Ṣ (fig. 72).
Datorită resistentei la înaintare, roţile vor fi aşezate într-o poziţie simetrică faţă de puntea spate, cu proiecţiile A şi A’ egale, precum este arătat în fig. 71; în mod normal, acest lucru se întâmplă dacă roţile sunt ghidate prin bare de direcţie.
Pe şosea, este posibil ca volanul şi direcţia să fie deviate din centru, fie către stânga fie către dreapta, în funcţie de înclinarea oblică a punţii. Pentru a repoziţionă direcţia pe centru, este necesar să se scurteze unul din braţele de direcţie şi să se lungească celalat, ceea ce ar duce imediat la deformatea paralelogramelor direcţiei.
Însă, când deviaţia punţii depăşeşte valoare de 1°, atunci geometria direcţiei este inevitabil afectată.
2)Axa spate este oblică în raport cu axa longitudinală a vehiculului cu o valoare Ṣ (fig. 73).

Pe şosea, roţile faţă se trag într-o poziţie simetrică cu proiecţiile lor asupra punţii spare A şi A’ egale, ceea ce înseamnă că barele de direcţie, centrul direcţiei şi centrul volanului corespund valorilor normale.
În acest caz, roţile spate sunt supuse unei alunecări negative sau pozitive, ceea ce cauzează uzura neregulată pe suprafaţa pneului.
Această orientare a direcţiei este valabilă atât timp cât unghiul Ṣ nu depăşeşte 1° + 1° 30′, valoare peste care vehiculul devine sensibil la cuplul motor, exprimat de raportul [cuplu motor]/[greutatea vehiculului].
Dacă acest raport este mare, roţile viratoare sunt trase într-o poziţie simetrică cu noua axă creată de roţile spate în modul descris în cele ce urmează:
Această variere se întâmplă în detrimentul centrulul de direcţie şi al centrului volanului, şi este imposibil de compensat deoarece este dinamică; acest efect caracteristic poate fi perceput pe şosea când, sub efectul cuplului motor, volanul îşi schimbă singur orientarea.
3)Există o deviere transversală S, nu oblică între cele două punţi (fig. 74). Acest tip de deviere poate să aibă loc atunci când, datorită distribuţiei neuniforme a greutăţii vehiculului, este creat un cuplu ce face ca roţile faţă să se rotească, în detrimentul centrului de direcţie şi al volanului; această condiţie poate fi creată când valoarea S depăşeşte 30-40 mm.
8.1 Efectele alunecarii asupra pneului
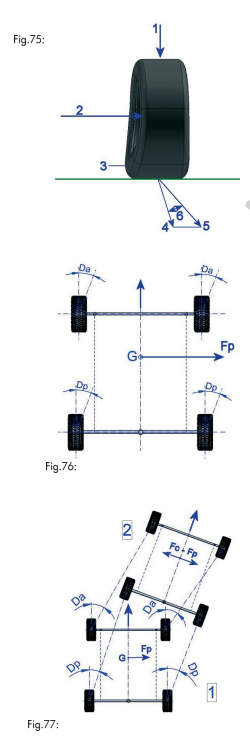
În capitolul în care am tratat geometria direcţie, s-a propus evaluarea comportamentului roţilor în timpul negocierii unei curbe la viteză mică, fără intererente. Dacă presupunem acum că vehiculul, în timpul negocierii curbei, este supus unor forţe perturbatoare precum viteza, vântul, cuplul motor şi frânarea, se va vedea că vehiculul nu urmează cu rigurozitate traiectoria corespunzătoare orientării roţilor; în schimb, va fi supus deviaţiilor datorită efectelor acestor forţe create asupra pneului. Acest efect este cunoscut ca ALUNECAREA PNEULUI (fig. 75).
Alunecarea pneului (a nu se confunda cu alunecarea roţii, tratată în capitolul despre convergenţă) este rezultatul deformaţiei elastică a pneului sub efectul forţelor perturbatoare; alunecarea poate de asemenea să fie creata dacă vehiculul merge în linie dreaptă, dar într-o măsură mai mică decât în curbe.
Unghiul de alunecare al pneului, precum se vede în fig, 75, este unghiul format pe planul orizontal de axa teoretică de direcţie a pneului şi axa efectivă:
-creşte o dată cu creşterea greutăţii asupra roţii;
-scade o dată cu creşterea presiunii pneului;
-poate varia mai mult sau mai puţin în funcţie de poziţia geometrică a roţilor.
8.2 Influenta alunecarii in timpul rularii in linie dreapta
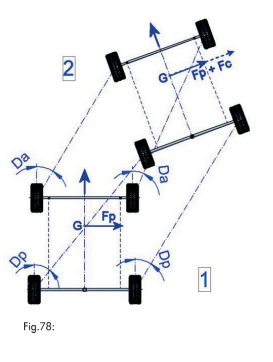
Cu referire la fig. 76, să presupunem că forţă perturbatoare Fp acţionează asupra vehiculului, iar punctul de aplicare al acesteia este centrul de greutate; generează o alunecare Da a roţilor faţă şi Dp a roţilor spate.
Ca şi consecinţă a forţei perturbatoare Fp, dacă alunecarea Da este mai mare decât Dp, vehiculul va avea tendinţa să înceapă să vireze către dreapta, ajungând din punctul 1 în punctul 2 (fig. 77), dar ca rezultat al acestui lucru, o forţă cetrifuga Fc este creată ce acctioneaza în sens contrar forţei Fp şi astfel devierea cauzată de alunecare nu mai are loc.
Acest comportament este cunoscut ca STABIL. Dacă, pe de altă parte, ca rezultat al aceleiaşi forţe perturbatoare Fp, alunecarea Dp este mai mare decât Da, vehiculul va avea tendinţa să înceapă să vireze spre stânga, ajungând din punctul 1 în punctul 2 (fig. 78). Forţa centrifuga Fc creată în acel moment, se va adăuga şi ea ca forţă perturbatoare. Vehiculul care tinde să crească deviaţia cauzată de alunecate este cunoscut ca INSTABIL.

8.3 Influenta alunecarii in timpul virarii
Într-o curbă, forţa centrifugă reprezentată de Fc, aplicată centrului de greutate G al vehiclului, produce deformări elatice laterale asupra penurilor; aceste deformări sunt legate de:
Distribuţia greutăţii pe punţi (schimbă punctul G de aplicare al forţei Fc);
Accelerarea şi decelerarea, indiferent de
rotile de aplicare al cuplului motor.
Dacă pneurile spate sunt supuse unei alunecări mai mari, vehicului va încerca să negocieze curba adoptând o rază mai mică decât cea impusă de roţile viratoare. În acest caz se spune că vehiculul este SUPRAVIRATOR.
Dacă pe de altă parte, pneurile faţă sunt supuse unei alunecări mai mari decât cele spate, traiectoria urmată de vehicul va avea o rază mai mare decât cea impusă de roţile viratoare; vehiculul tinde să iasă în curbă şi se spune că vehiculul este SUBVIRATOR.
Pentru a corecta aceste alunecări, sau să le facă folositoare, producătorul a încercat să redistribuie greutatea, pentru a stabili care penuri şi la ce presiune trebuiesc folosite pentru a adapta poziţia geometrică a vehiculului la cerinţele şoferului, astfel încât vehicului să fie echilibrat corect.
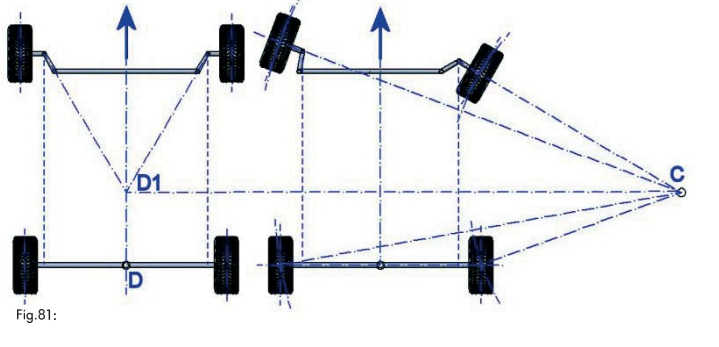
Toate aceste unghiuri caracteristice ale vehiculului influenţează alunecarea şi deci comportamentul dinamic al vehiculului; pentru că fenomenul este unul foarte complex, este dificil să îl tratăm în totalitate în acest document, dat fiind numărul mare de diferenţe structurale între dferitele tipuri de maşini, un exemplu va fi dat al corecţiei dinamice a unui vehicul aflat într-o curbă. În primul caz, care este teoretic, punctul de convergenţă al barelor de direcţie coincide cu centrul punţii spate, punctul D (fig. 80) În al doilea caz, însă, prin mutarea punctului de intersesctie al barelor de direcţie în faţa punţii spate, punctul D1, atunci poziţia centrului curbei se schimbă de asemenea; în acest caz, se crează o corecţie dinamică, cauzând deformări elastice diferite.

8.4 Alunecarea primara si secundara
Pneurie radiale moderne, datorită caracteristicilor structurale, produc un efect de alunecare care este independent de forţele externe ce ar putea interveni pentru a le deforma elastic.
Această alunecare este divizată în două
categorii:
1 ALUNECAREA PRIMARĂ – are loc atunci când deformarea laterală elastică a pneului este generată de asimetria structurală a anvelopei în raport cu planul latitudinal al roţii; de fapt, sârmele ce formează anvelopei a pneului nu sunt perpendiculare pe suprafaţa de rulare ci oblice; alunecare primară va fi spre stânga sau dreapta, în functie de orientarea sârmelor ce formează zona laterală cea mai apropiată de suprafaţa de rulare, şi această tendinţă este inversată dacă se inversează direcţia de rotaţie a roţii.
ALUNECAREA SECUNDARĂ – are loc
când deformarea laterală elastică a pneului este generată de asimetria în rigiditatea laterală a pneurilor, asimetrie cauzată de defecte de fabricare.
Dacă aceste două fenomene sunt accentuate, pot afecta direcţia vehiculului în linie dreata, fiind constant nevoie de corectarea direcţiei de mers. Un fenoment similar a fost observat în capitolul în care am vorbit despre înclinarea pivotului; aşadar, dacă este detectată în timpul verificărilor şi corecţiilor unghiurilor roţilor, atunci trebuiesc luate în seama ambele fenomene ca şi cauze ale direcţie necentrate.
În acest caz, pentru a remedia problema, unghiul de fugă al roţilor viratoare trebuie să fie pe cât posibil egal, iar o verificare amănunţită este necesară pentru a se vedea dacă există vreo forţa rezistenţă ce acctioneaza asupra acestora, precum, de exemplu, frâne, presiuni ale pneurilor diferite sau uzura diferită ale acestora.